6. MAJOR SCALES AND THE HARMONIC WHEEL

The Major scales are obtained with the Harmonic Wheel by simply rotating its two discs until the sign  matches the desired tonic. The remaining notes in the scale are then automatically marked with the sign . As an example, Fig. 6 shows the D Major scale.

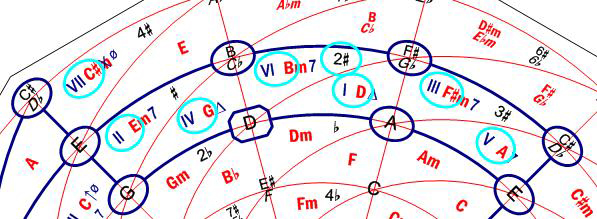
Figure 6. D Major scale.

On the other hand, the lines in DARK BLUE indicate the region in the Harmonic Wheel embraced by this scale (the use of which will be seen in Chapter 13). For every Major scale, this region is a curved rectangle.

The notes in the scale thus marked are represented in black (because this colour always represents notes) and they are placed by following the consonance relationships. Therefore, they are not sorted out by their pitch. If we want to have these notes sorted out by their pitch, we must use the red notation (although what this colour actually represents are chords, as will be explained in Level 2). This way, the notes are found to the right of the Roman numerals, which indicate the scale degrees, as in Fig. 6. When using this notation, we must neglect the letters and symbols appearing to the right of the notes.

In Fig. 6 we can also see, next to the I degree (Tonic), the key signature of this scale, that is, 2 sharps. If we continue rotating the two discs forming the Harmonic Wheel, we will see how the different scales appear, along with their tonics and key signatures. So, note that, when augmenting the number of sharps or reducing the number of flats, the tonics appear, precisely, by Perfect fifths. And, when reducing the number of sharps or augmenting the number of flats, the tonics appear in the reverse order, that is, by Perfect fourths.

An interesting property of the Major scale is that, if we represent its notes on a circumference, they will be located one next to the other and they complete a half circumference. As an example, Fig. 7 shows this kind of representation for the D Major and A Major scales. This fact means that the 7 notes of a Major scale can be sorted out by Perfect fifths, although in this case the first note is the IV degree, that is, the Subdominant (G in the first scale and D in the second one). The fact that the notes in a Major scale are connected by Perfect fifths indicates the high degree of consonance among them. In Fig. 7, notice that those enharmonic notes not following the series of P 5^th intervals are discarded.

Figure 7. The D Major and A Major scales represented on a half circumference.

Furthermore, in this representation it can be clearly seen how the altered notes appear. Thus, in the D Major scale, which has a key signature with 2 sharps, the notes F and C appear at the end and following the order of sharps. And, when going from the D Major to the A Major scale, we can see that the note G is replaced by G, as must occur, since the A Major key signature has 3 sharps. This way, it can be observed that the sharps appear by Perfect fifths, beginning with F. And, when augmenting the number of sharps in the key signature, the tonics also appear by Perfect fifths. On the other hand, if we represented the scales containing flats, we would see how the flats appear by Perfect fourths, beginning with B; and that, when augmenting the number of flats, the tonics also appear by Perfect fourths.

Learning the scales takes its time. Firstly, the order of sharps and flats must be known. And then, it is necessary to know how the key signatures are related to the tonics. To do this, the following two rules apply and can be easily proved by representing the scales as in Fig. 7:

1. In key signatures containing sharps, the last sharp note is the Leading tone. For example, in the key signature having 3 sharps, they correspond to F, C and G. Thus, G is the Leading tone and A is the Tonic. Therefore, this key signature corresponds to the A Major scale.
2. In key signatures containing flats, the next to last flat note is the Tonic. For example, in the key signature having 5 flats, they correspond to B, E, A, D and G. Thus, D is the Tonic and this key signature corresponds to the D Major scale.

We only have to add to these rules that the key signature having no accidentals corresponds to the C Major scale and that having one flat corresponds to the F Major scale. A musician must be able to play every scale both ascending and descending, by only knowing the tonic and the key signature, finding the notes mentally. Although the Harmonic Wheel allows us to understand the scale construction and to solve any doubt related with them, it cannot replace the necessary practice to fluently play all the scales.

It is difficult to exaggerate the importance of Major scales in Music. In fact, the whole musical script system is conceived to easily write this type of scales. Thus, when learning this system, one can realize that, for a given staff with any clef and any key signature, if there are no accidentals, all the written notes necessarily belong to a certain Major scale. On the contrary, the notes out of this scale will have accidentals. This way, the accidentals serve to easily recognize the notes not belonging to the considered Major scale. On the other hand, all the diatonic instruments (some types of flutes and harmonicas, almost all the toy instruments, etc.) only contain the notes of a Major scale.