13. CHORD FINDER AND THE MAJOR-MINOR SYSTEM

In the last chapter, it was pointed out that knowing the chords associated to any scale is extremely important and we also saw the big difficulties related to it. If we go back to Table 4 or Fig. 18 and we pay attention to their second part, that is, that showing the 3 note chords, we will see that the first 6 chords are consonant and the last one is dissonant. The Harmonic Wheel allows us to obtain the consonant chords of any scale in an automatic way. We will show it with an example:

If we choose the C Major scale (Fig. 19), the DARK BLUE LINES show the region in the Harmonic Wheel embraced by this scale, which is a curved rectangle. Precisely inside this region, there are the consonant chords associated to the C Major scale, that is, the 3 Major chords F, C, G and the 3 minor chords Dm, Am, Em. Each of these chords is preceded by a Roman numeral indicating its corresponding scale degree.

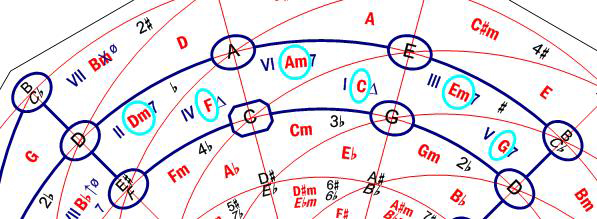
Figure 19. Consonant chords associated to the C Major scale.

Furthermore, in this representation we can observe that the chords C and Am have a “central position” in the C Major scale. If we now pay attention to the 3 Major chords, we see that the F chord (Subdominant) is located to the left of C (Tonic), that is, towards a key signature with more flats, so it is said that the Subdominant Chord has a regressive character. On the contrary, the G chord (Dominant) is located to the right of C, that is, towards a key signature with more sharps, so it is said that the Dominant Chord has a progressive character.

The analysis of the 3 minor chords is completely analogous. Thus, the Dm chord is located to the left of Am, so having a regressive character with respect to it. And the Em chord is located to the right of Am, so having a progressive character with respect to it. These 3 chords, Dm, Am and Em correspond to degrees II, VI and III, respectively. However, if we consider these 3 minor chords inside the A natural minor scale (relative of C Major), then the Am chord will be the Tonic chord (I degree), Dm the Subdominant (IV degree) and Em the Dominant (V degree). Therefore, the great symmetry that exists between the 3 Major and the 3 minor chords associated to a Major scale is apparent. The deep relationship between a Major scale and its relative minor scale is now evident, too. The corresponding chord for the VII degree, that is, the Bm(5) did not appear in this analysis, for it is not a consonant chord, but a dissonant one.

Looking at Fig. 19 again, we can say that the 7 notes of a Major scale are the minimum necessary to form 3 Major chords in intervals of P 5^ths: one “central” chord and, with respect to it, one regressive and one progressive chord. This provides this set of 7 notes with a strong cohesion and unity, and establishes the particular succession of whole and half steps among them as well. Moreover, with the same 7 notes we can form other 3 minor chords, in intervals of P 5^ths, too: one central chord and, with respect to it, one regressive and one progressive chord. These facts justify both the existence of the Major and its relative minor scales and, at the same time, confer these two modes a supremacy with respect to the other 5.

As we saw, the representation of notes and chords provided by the Harmonic Wheel allows us to easily understand which is the underlying relationship connecting the 7 notes composing a Major scale, that is to say, which is the origin of its particular succession of whole and half steps, the reason why two relative modes are established, the Major and the minor, and which are the main characteristics of the chords associated to them. All this information is not visible in other kinds of representations, even in that of Fig. 18, where the standard music script was used. This is a consequence of the particular design of the Harmonic Wheel, which is based on the most fundamental relationships among sounds, that is, the consonance relationships.

Anyway, once one has seen and understood this analysis, he will find very logical that Western music evolved with time towards the Major-minor system, where the tonics of these two modes are precisely the roots of the two chords having a “central position” (from the point of view of consonances) in the Major scale.

Let us go on considering the 4 note chords associated to the Major scale, that is, those in the last part of Table 4 and Fig. 18. Their localization in the Harmonic Wheel is automatic, too, since to the right of each chord there is a symbol indicating the chord type (Fig. 20).

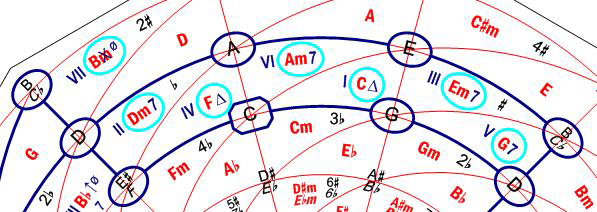
Figure 20. 4 note chords associated to the C Major scale.

By rotating the two discs forming the Harmonic Wheel, we will find the chords associated to any Major scale. But this powerful and versatile musical abacus also implements the minor scales: natural, harmonic and melodic. So, by means of a similar procedure, we will find every chord associated to any minor scale.

The option given by the Harmonic Wheel to obtain the chords associated to any scale is called CHORD FINDER function. And this function is not restricted to the Major and minor scales, but it is also valid for other types of scales that will be explained later (Chapters 15 and 16). Moreover, due to the graphic nature of the scale and chord representations, it is very simple to determine which chords are nearer to or further from a given scale, that is, if they contain some notes belonging to the scale or, on the contrary, they are completely unrelated to it.