4. INTERVALS AND THE HARMONIC WHEEL

Determining the interval between any two notes is one of the first obstacles arising when one begins the study of Music. Nevertheless, this task is highly simplified by using the Harmonic Wheel, as we will see in this chapter.

In the Harmonic Wheel, the Musical Notes are represented in BLACK and the couples of enharmonic notes are represented by placing one of them just above the other. On the other hand, the notes are placed in such a way that each note is connected, by means of red lines, with the 6 notes with which it forms Consonant Intervals.

As previously explained, the Consonant Intervals are combinations of 2 notes that, when played together, produce a sensation of harmony, rest and stability. And, apart from the unison and the octave, they are the P 5^th, the M 3^rd and the m 3^rd, as well as their inversions.

In the Harmonic Wheel, each of these consonant intervals is represented with a different type of line. Thus, Circumferences are used for P 5^th intervals (and their inversions, P 4^ths); Radii, for m 3^rd intervals (and their inversions, M 6^ths); and Spirals, for M 3^rd intervals (and their inversions, m 6^ths). Fig. 3 shows these three types of lines.

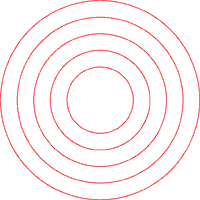
Circumferences: P 4th, P 5th

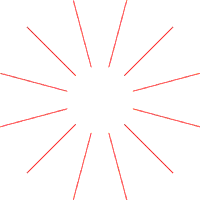
Radii: m 3rd, M 6th

Spirals: M 3rd, m 6th

Figure 3. Lines used to represent the consonant intervals.

As an example, Fig. 4 shows the note E and the 6 notes with which it forms consonant intervals, which are:

• A and B, at intervals of P 4^th and P 5^th, respectively, and located on the circumference going by note E. If we move to the right along this circumference, we find P 5^th intervals, while if we move to the left, we find P 4^th intervals. (The enharmonic C is discarded, for it does not form a 5^th interval with E, but a 6^th).
• G and C, at intervals of m 3^rd and M 6^th, respectively, and located on the radius going by note E. If we move upwards along this radius, we find M 6^th intervals, while if we move downwards, we find m 3^rd intervals. (The enharmonic D is discarded, for it does not form a 6^th interval with E, but a 7^th).
• C and G, at intervals of m 6^th and M 3^rd, respectively, and located on the spiral going by note E. If we move to the right along this spiral, we find M 3^rd intervals, while if we move to the left, we find m 6^th intervals. (The enharmonic A is discarded, for it does not form a 3^rd interval with E, but a 4^th).

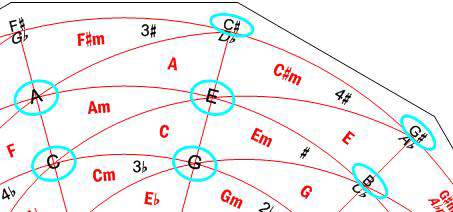
Figure 4. The note E and the 6 notes with which it forms consonant intervals.

NOTE: All the indications in LIGHT BLUE are included for illustrative purposes and do not appear on the Harmonic Wheel.

Furthermore, these 3 types of lines allow us to easily know the interval between any two notes. To do this, we only have to pay attention to the Major (3^rd and 6^th) and Perfect (4^th and 5^th) intervals. The orientations of these intervals with respect to a given note are always the same and are easy to memorize. Fig. 5 shows these intervals from note E.

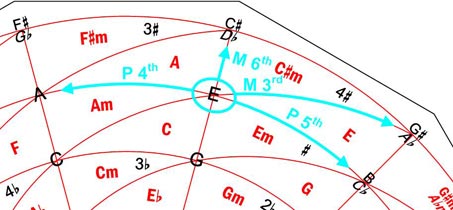
Figure 5. M 3^rd, P 4^th, P 5^th and M 6^th intervals from note E.

By comparison with these 4 intervals, it is possible to determine which is the interval between E and any other note, except in the case of a 2^nd or its inversion, a 7^th. But, for these two cases, it is sufficient to remember that the M 2^nd contains 1 W.

The final procedure consists in firstly determining the interval number of the given interval and then its quality. If keeping to this order, it will not be necessary to deal with enharmonic notes. Let us see some examples:

• Which is the interval between E and G? It is a 3^rd. So, we follow the M 3^rd line and compare with the G at its end. As it is a G, this means that between E and G there is a M 3^rd, so between E and G there is a m 3^rd.
• Which is the interval between E and C? It is a 6^th. So, we follow the M 6^th line and compare with the C at its end. As it is a C, this means that between E and C there is a M 6^th, so between E and C there is a m 6^th.
• Which is the interval between E and B? It is a 5^th. So, we follow the P 5^th line and compare with the B at its end. As it is a B natural, this means that between E and B there is a P 5^th, so between E and B there is a d 5^th.
• Which is the interval between E and A? It is a 4^th. So, we follow the P 4^th line and compare with the A at its end. As it is an A natural, this means that between E and A there is a P 4^th, so between E and A there is an A 4^th.
• Which is the interval between E and D? It is a 7^th. Its inversion, from D to E, contains 0.5 W, so it is a m 2^nd. Therefore, between E and D there is a M 7^th.

In case the first note in the interval is altered, we will begin by considering this note natural and then we will include the effect of the accidental. Let us see a couple of examples of this:

• Which is the interval between E and G? We begin by considering the interval between E and G, which is a 3^rd. And, following the previous procedure, we see that it is a M 3^rd. Therefore, between E and G there is an A 3^rd.
• Which is the interval between E and A? We begin by considering the interval between E and A, which is a 4^th. And, following the previous procedure, we see that it is a d 4^th. Therefore, between E and A there is a dd 4^th.