LEVEL 2: FOUNDATIONS OF HARMONY

9. MAJOR AND MINOR CHORDS

A Chord is a set of 3 or more notes that sound simultaneously. In a similar way as we saw with the intervals, there are some combinations of 3 notes that, when played together, produce a sensation of harmony, rest and stability. They are the so-called Consonant Chords and there are only two types of them: Major and minor Chords. The rest of the chords are Dissonant.

A Major Chord is built by superimposing a M 3^rd and a m 3^rd intervals on a note which is called the Root. And a minor chord is built by superimposing first a m 3^rd and then a M 3^rd.

Thus, for example, the C Major chord is composed by notes C, E, G; and the A minor chord is composed by notes A, C, E. In both cases, it can be seen that, between the first note (that is, the root) and the last one, there is a P 5^th interval (C – G in the first case and A – E in the second one), which makes these chords especially stable. The C Major chord is simply represented by “C”, while the A minor chord is represented by “Am”.

Those people who play polyphonic instruments, such as piano, guitar, etc., must learn to play these types of chords, as well as other types that will be described in the next chapters. Moreover, they must learn to play the notes composing these chords successively, both ascending and descending, what is known as Arpeggios. On the contrary, those people who play monophonic instruments, such as trumpet, saxophone, etc., can only play the arpeggios, but not the chords. Anyway, both the former and the latter must learn to recognize the different types of chords “by ear”.

On the Harmonic Wheel, the Consonant Chords, that is, Major and minor chords, are shown in RED and are placed inside curved triangles. The notes composing these chords, that is, their arpeggios, are placed just at the vertices of these triangles.

In Fig. 11, we can see how the notes composing the C and Am chords are so easily found by using the Harmonic Wheel.

Figure 11. The notes composing the C and Am chords (consonant) are placed at the vertices of curved triangles.

The two chords considered in this example contain the note E. If we look for all possible Major and minor chords containing that note, the answer again is very simple: They are those chords surrounding the note E (Fig. 12), that is: E, Em, C, Am, A and Cm.

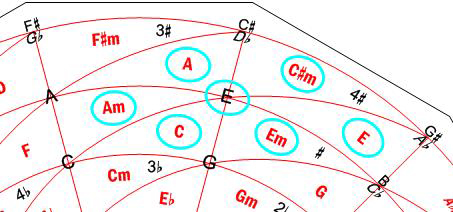
Figure 12. Obtaining all Major and minor chords containing the note E.