|
5. MAJOR SCALES
In Chapter 1, we saw that the C Major scale is composed by the following succession of notes and intervals:
C Major scale
The first note in the scale is called Tonic (in this example, C) and it is normally repeated at the end of the scale. The numbers representing the order of each note in the scale are called scale degrees and are written in Roman numerals:
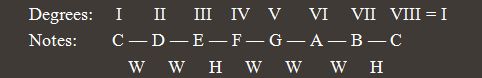
C Major scale, along with its degrees
The names of the scale degrees are the following:
| Degree |
Degree Name |
| I |
Tonic |
| II |
Supertonic |
| III |
Mediant |
| IV |
Subdominant |
| V |
Dominant |
| VI |
Superdominant |
| VII |
Leading tone |
| VIII |
Octave or Tonic |
If we want to build a Major scale beginning, for example, with note A, that is, the A Major scale, we only have to keep to the same succession of whole and half steps seen for the C Major scale, that is, W W H W W W H:

A Major scale
Therefore, we can define a Major Scale as a set of 7 notes characterized by the whole and half step succession W W H W W W H. Another equivalent way to build the Major scale consists in finding the notes forming Major or Perfect 2nd to 8th intervals with the tonic.
In the A Major scale, we can observe that there are 3 sharp notes (C, F and G), which is necessary to keep to the whole and half step succession. The number of sharps or flats in a Major scale is known as the Key Signature. So, it is said that the A Major key signature has 3 sharps.
The order in which the sharps appear in Major scales is always the same: F, C, G, D, A, E, B (that is, by P 5th intervals). This means that, in a Major scale having 3 sharps, they will correspond to the notes F, C and G, as seen in the A Major scale. In the same way, if a scale only has 2 sharps, they will correspond to the notes F and C, as occurs in the D Major scale:
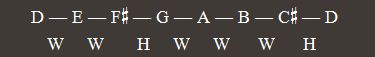
D Major scale
On the other hand, the flats appear in the reverse order with respect to the sharps, that is, in the order: B, E, A, D, G, C, F (that is, by P 4th intervals). So, in a scale having 2 flats, they will correspond to the notes B and E, which occurs in the B Major scale: Major scale:
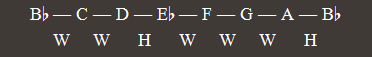
B Major scale Major scale
Building the Major scales, determining the key signature of each of them or knowing the order in which the tonics appear when augmenting or diminishing the number of sharps or flats, are complex questions that require much time of study. For this reason, the Harmonic Wheel is provided with a very easy system to solve all these questions directly and in a very educational way. To do this, we only have to rotate the two discs forming this instrument, as we will see in the next chapter.
|